2009�N3��16��(��)����19��(��)�ɂ����čs�����v���O�������h2009�t�̓��e�̂܂Ƃߌ��ł��B
1���ڂ͂܂��A���ꂼ���PC��C�v���O���~���O���ł���悤���\�z���A�R���p�C���̎d������{���@�Ȃǂ̊�b�I�Ȃ��ƂJ�Ɉ����Ȃ���A���ۂ������ϕ��̐��l�v�Z�����Ă��炢�܂����B
���\�z
�قڑS���̎Q���҂�C�R���p�C���������Ă��Ȃ��������߁A�����炪�\�ߗp�ӂ��Ă������C���X�g�[����z�z���Ċ��\�z��Ƃ��s���܂����B�R���p�C����GCC�ŁAEquation Solution�ɒu���Ă���win�p�C���X�g�[����20090206��(gcc-4.4-20090206-32.exe)�𗘗p���܂����B
���ɁA�v���O�����쐬������s�܂ŁB���Ƀe�L�X�g�G�f�B�^�̐����͕s�v�ł������A�R���p�C���A�v���O�����̎��s�̎d���ɂ��ẮA��͂葶�݊����Ȃ��g���Â炢Windows���R�}���h�v�����v�g�ɂ��Ă����炩�������K�v�ł����B
Windows�W�����R�}���h�v�����v�g��cmd.exe�Ƃ������O�ŁA"cmd"���t�@�C�������w�肵�Ď��s�������ƂŋN���ł��܂��BVista�Ȃ�A�t�H���_�̃A�h���X�o�[��"cmd"�Ɠ��͂���A���̃t�H���_����ƃt�H���_�ɂȂ�����ԂŃR�}���h�v�����v�g�������オ��̂ŕ֗��ł��B
��b���@
C�������b���@�ɂ��ĊȒP�Ɉ����܂����B�����ł����������̓��e�ɂ��ďڂ����͏����܂���B
- �e���v���[�g(���܂��Ȃ�)
- #include
- int main(void){�`}
- ��(�^B function(�^A a, ...){�`})
- �ϐ�(�^A x=�����l;)
- �o��(printf����)
���ۂɂ́A���������ϕ��̐��l�v�Z�̃v���O���������ۂɑg�މ��K�ƕ��s���ĕK�v�Ȏ��_�ʼn�����܂����B
���l�v�Z(�����ϕ�)
���l�v�Z�Ƃ́A���w�I�E�����I�Ȍ����������߂�(��͓I�ɉ���)���Ƃł͂Ȃ��A�߂��l�̉������߂�(���l�I�ɉ���)�����������܂��B���Ɍ���ł́A�ߎ������R���s���[�^��p���Čv�Z�������Ƃ��w�����Ƃ������ł��B
�����ϕ��̐��l�v�Z�ɂ����ẮA�Ɍ��̍l�����Ōv�Z���܂��B��̓I�ɂ́A���̂悤�Ȏ��ŋߎ����܂��B
- �����W��
- ��ϕ�
���̂悤�ɁAh����x���\�����ƂȂ�悤�Ɏ�邱�Ƃŋߎ�����l�����ŁA�O�p���̔�����ϕ������Ă��炢�܂����B
���������ƂɁA���ݕ����傫������Ƌߎ����x�������Ȃ�A�t�ɏ��������Ă��R���s���[�^�̌v�Z���e�͈͂��z���Ă��܂��܂��B�������������_���������邽�߁A��萸�x�̂悢�A���S���Y����ߎ���������������܂����A�P���̂��߂���ȏ�͈����܂���ł����B
2���ڂ�1���ڂ̔��W�Ƃ��āA����Ɏ��p�I�Ȕ����������̐��l�I��@�������܂����B
�I�C���[�@
�I�C���[�@�Ƃ́A(1�K�̏�)�����������Ƃ��̏����������^����ꂽ���ɁA���W�I�ɂ��̐��l�������߂�ł��V���v���ȕ��@�̂ЂƂ��ł��B(�P���䂦�ɐ��x�͔��Ɉ���)
�Ⴆ���镨��(�ʒux)�̑��x���������Ă���A�܂����������
���^�����Ă��鎞���l���܂��B��������(����t=t_0�ɂ�����ʒux=x_0)���^�����Ă���A���̕��̂̈ʒu�̎��Ԕ��W�����̂悤�ɃV�~�����[�g���邱�Ƃ��ł��܂��B�����̋ߎ������ό`���������ł����A����t�ɂ����镨�̂̈ʒux�Ƒ��xf(x,t)����A���ԃ�t��̕��̂̂��悻�̈ʒu��������܂��B
1���ړ��l�ɎO�p�����Ƃ��Čv�Z���Ă��炢�܂����B���R�A����������ۂ��ĐU�����錋�ʂ�������̂ł����A1���ߎ��̂��߂����x�������Ƃ������Ƃ��m�F���Ă��炢�܂����B
�����鉻(Visualize)
���������Ȃ̂ŁA���ʂ�CSV�o�����ăG�N�Z���̃O���t�ɂ�����@�������܂����B
while ( t < 10.0 ) {
printf( "%f,%f", t, x );
x = x + dt * f(x,t);
t = t + dt;
}
�Ⴆ�Ώ�̂悤�ɁA���[�v����printf���ŃJ���}���ɒl��\������悤�ɂ��Ă����܂��B���̃v���O�������R���p�C�����āA���ʂ��o�͂���ɂ͎��̂悤�ɂ��܂��B
| �R�}���h1 | ���� | a.exe > output.csv |
|---|---|---|
| �o�� | ���R�}���h�v�����v�g��ɂ͉����\�����ꂸ�Aoutput.csv�Ɍ��ʂ��ۑ������ |
�W���ł�CSV�t�@�C���̓G�N�Z���ŊJ���悤�ݒ肳��Ă���̂ŁA�o�͂��ꂽCSV�t�@�C�����_�u���N���b�N����G�N�Z���ŊJ���O���t����邱�Ƃ��ł��܂��B
4���̃����Q=�N�b�^�@
���܂ł̍l�����͐��x�����Ɉ������̂ł��邽�߁A���ۂɗ��p����邱�Ƃ͂��܂肠��܂���B����ɑ��āA(4����)�����Q=�N�b�^�@(RK4)�ƌĂ����@�͐��x���悭�A���̕��@��(��)�����������������Ɖ��̔��U�����}���邱�Ƃ��ł��܂��B
2���ڂ̎��Ԃ��c�菭�Ȃ��������Ƃ�����A�����̍��h�Q���҂�RK4�����������邱�Ƃ��ł����̂�1�l�����ł����B
3���ڂ́A������p�����吔�̖@���������e�J�����@�������܂����B
����
C����ɂ�rand()�����W���ŗp�ӂ���Ă��āA0����32767(16�i����0x7FFF)�܂ł͈̔͂̐����������_���ɕԂ��܂��B[0,1)��Ԃ̗��������ꂩ��K�v�Ȃ̂ŁA�܂���[0,1)��Ԃ̎����������_���ɕԂ��������A�g�p���Ă��炢�܂����B
double frand(void) {
return (double)rand()/0x8000;
}
�����e�J�����ϕ�
�吔�̖@���ɂ��A���s��������J��Ԃ��Ď��ۂ��N�������s�Ŋ���A���ۂ̊m���ɋ߂Â��܂��B����𗘗p���Đϕ��̒l�����߂�̂������e�J�����ϕ��ł��B���h�ł́A�����e�J�����@�ɂ��P�ʎl���~�̖ʐς������̑�G�c�Ȓl�����߂܂����B
[0,1)^2�̌�P�������_����鎎�s���l���܂��B���̂Ƃ��A�_P���P�ʎl���~D := {(x,y) | x,y>0, x^2+y^2��1} �Ɋ܂܂�鎖�ۂ̊m���́A�ʐϔ�Ɠ�������/4�ɂȂ�܂��B����āA���s���\���Ȑ������s���Ċm�����v�����A4�{��������̑�G�c�Ȓl�����߂邱�Ƃ��ł��܂��B
���̂悤�ɁA�����e�J�����@��p����(�d)�ϕ��̒l���r�I�ȒP�ɋ��߂邱�Ƃ��ł��܂��B�������A��l�ȗ����ŏ\���Ȏ��s���s��Ȃ���ΐ��m�Ȓl�͓���ꂸ�A1���ߎ��ق������͂悭����܂����B
��r�I�S������Ȃ芮��������ꂽ�̂ŁA���s������ɑ��₵�Čv�Z���Ă��������A�l���~�����̓_P�̍��W��CSV�o�͂��ăG�N�Z���ŎU�z�}��`���Ȃǂ��Ă��炢�܂����B
�C�̕��q�^�����f��
�����e�J�����@��p����A�m�����f���̎��Ԕ��W�ׂ邱�Ƃ��ł��܂��B�Ⴆ�Ύ��̂悤�ȋC�̕��q�^�����f�����l���܂��B
- ��̗e��V_1,V_2(���̐�)������A�P�ʎ��ԓ�����1�̋C�̕��q�����ʉ߂ł��Ȃ��ʘH(��)�Ōq����Ă���Ƃ���
- �C�̕��q�͑S�Ă�N����AV_n�̕��q����N_n�Ƃ���
- ���߂�N_1=N, N_2=0
-
�P�ʎ��ԓ�����ɋC�̕��q��V_1����V_2�ֈړ�����m��
frand()�œ���������p_1�ȉ��ł����V_1����V_2�ցA�����łȂ����V_2����V_1��1�̕��q���ړ������ƍl���܂��B���̂悤�Ȏ��s���\�����J��Ԃ����ƂŁA�C�̕��q�̉^���̎��Ԕ��W�A�܂��C�����t���V�~�����[�g���邱�Ƃ��ł��܂��B
��Ƃ��Ă͒P�����������f���������܂������A��茵���ȃ��f�����̗p���Ă���������悤�ɒ��ׂ邱�Ƃ��ł��܂��B���܂莞�Ԃ͂���܂���ł������A�e���3�ɂ���Ȃǂ̑��̃��f���ł������Ă��炢�܂����B
4���ڂ��Z���I�[�g�}�g���ECG�������܂����B�{����C��Ruby��CG��������Ƃ悩�����̂ł����A���C�u������p�ӂ����肷�鎞�Ԃ��Ȃ������̂ŁAScheme���C���ł��B
�Z���I�[�g�}�g��
�ȒP�Ɍ����ƁA�Z���I�[�g�}�g�������C�t�Q�[���̂���ʓI�E�w�p�I�ȑ��̂ł��B���C�t�Q�[���͕���2�����ł����A�����1�����̃Z���I�[�g�}�g���������܂����B
�����Z��������ł��āA�X�̃Z���������E���S�̂ǂ��炩�̏�Ԃ����܂��B���鎞���ɂ����āu�����v�̃Z���́A�������ׂ̃Z�����u�����v�Ȃ�Ύ��̎����ɂ́u���S�v����(�ߖ���)�Ƃ����悤�����[�������܂��B�����ăZ���̏�����Ԃ�^���A���[���Ɋ�Â������Ԕ��W��}�����܂��B����ƃ��[���ɂ���Ă��t���N�^���}�`���o���オ������A�F�X�Ƌ����[�����ʂ��܂��B
���̃��[���́A�Z����������1�A���S��0�Ɠ��ꎋ(��i�\��)���邱�ƂŁA�ȒP�ɔz��Œ�`���邱�Ƃ��ł��܂��B���[���̗�����̕\�Ɏ����܂��B���̕\�ł́A�����Z�����u���v�A���S�Z�����u���v�Ő}�����Ă��܂��B
| �C���f�N�X | ��i�\�� | �Z�� | ���Z�� |
|---|---|---|---|
| 0 | 0b000 | ������ | �� |
| 1 | 0b001 | ������ | �� |
| 2 | 0b010 | ������ | �� |
| 3 | 0b011 | ������ | �� |
| 4 | 0b100 | ������ | �� |
| 5 | 0b101 | ������ | �� |
| 6 | 0b110 | ������ | �� |
| 7 | 0b111 | ������ | �� |
- �}1: �Z���I�[�g�}�g���̎��Ԕ��W�}

���̃��[����̏ꍇ�A{0,1,1,0,1,1,0,0}�Ƃ����z��(Scheme�̏ꍇ�Ȃ�'(0 1 1 0 1 1 0 0)�Ƃ������X�g)���������̂ł��B���݂̃Z���y�їאڂ���Z��(3���)�̏����i�\��(2���)�ƌ��Ȃ�10�i���̐����ɒ���(1���)�A���[���z��(���X�g)�̂��̔ԍ��̗v�f�����̃Z���̏��(4���)�Ƃ��čX�V��������̂ł��B
�������AC����ȂǂŕW���o�͂��邱�ƂŎ��Ԕ��W�ׂ邱�Ƃ��ł��܂��B�������ǂ����Ȃ��O���t�B�b�N�X�ɂ��Ă݂����ł���ˁB�i�}1�́A��̃��[����1�̃Z�����������Ă��鏉����Ԃ���n�߂����́j
CG (with Scheme)
��b������K��Scheme�Ɋ���Ă���Q���҂����������̂ŁA��b�͏Ȃ���Scheme�ŃO���t�B�b�N�X���������@�̕��K�������܂����BScheme���O���t�B�b�N�X���������߂ɂ́A�܂��v���O�����̎n�߂Ɏ��̂悤�ɏ����܂��B
(require (lib "graphics.ss" "graphics")) (open-graphics) (define w (open-viewport "Cellular Automaton" 500 500))
�����āAw�ɑ�����, �l�p, �ȉ~, ���p�`��`���ɂ́A���̂悤�Ȗ��߂��g���܂��B�Ȃ��}�`���߂œ�����h��ׂ��ꍇ�́Adraw-�`�ł͂Ȃ�draw-solid-�`�Ƃ������߂��g���܂��B
((draw-line w) (make-posn x1 y1) (make-posn x2 y2) "color")
((draw-rectangle w) (make-posn x y) width height "color")
((draw-ellipse w) (make-posn x y) width height "color")
((draw-polygon w) (list (make-posn x1 y1)
(make-posn x2 y2)
;
(make-posn xn yn) )
(make-posn x0 y0)
"color" )
���h�ł͐��̕`�������������܂���ł������c�cf(^^;
���h1���ڂ��I��������A2���ڂɎQ���ł��Ȃ��l�̂��߂ɉۊO���Ƃ��s���܂����B2�l�̎Q���҂�RK4������������Ƃ���܂ōs���܂����B
�܂��AScheme�Ő��l�v�Z������ۋC������Ɠ�����d�l�������܂����BScheme�ł������^���L�����^�����m�ɕ�����Ă��āAC���l���L�����������݂��������^�ƈႢ�A�L�����^�ł��f�[�^��2�̐���(���q/����)�ɕ����Ĉ����܂��B�����Scheme�ł͓����I�����z�������𗘗p���Ă���AC����ƈႢ����Ȍ��̐����f�[�^�i�A�����̕��x���j���������Ƃ��ł��܂��B�䂦���L�����^�̐��x�����ɋ���ł��B
�v�Z���Ɉ�x�ł������^�̒l��p����Ƃ��̌��ʂ������^�ɂȂ�܂����A�L�����^�݂̂Ōv�Z�����Ă������͌v�Z���ʂ��L�����^�ł���A�]�����v�Z�̐��x��L�����^�̐��x�ɕۂ��Ƃ��\�ł��B���ݕ����\�����������Ȃ���ΐ��x���Ȃ������ϕ��̌v�Z�ɂ����āA���̐����͔��ɋ��͂ł��B�����^�ō��ݕ�����������������Ƃ����ɒl���v�Z�s�\�Ȕ͈͂ɒB����̂ɑ��A�L�����^�͂��̌v�Z�\�͈͂��q��ł͂Ȃ��̂ł��B
���x�̈��������^�̒l�x�̗ǂ��L�����^�֕ϊ����邽�߂ɂ́Ainexact->exact���߂��g�p���܂��B���̖��߂͎����ȊO�ł��A�s���m�Ȓl�𐳊m�Ȓl�֕ϊ����邽�߂Ɏg�����Ƃ��ł��܂��B
(inexact->exact pi) (inexact->exact 1.25+i5.00)
���ɂ����h���A��������肵���Ƃ��Ɉȉ��̂悤�Ȃ��Ƃ������܂����B
- [C] FILE�^�̈����A�W�����o�͂Ƃ̈Ⴂ
- [C] �z��ƃ|�C���^�̈����E�l����
- [C] �^�̋����ϊ�(�L���X�g)
- [Scheme] lambda�Ɗ��K�p
- [Ruby] �Y��A�L�[�{�[�h���́A�t���O�̎g����
- �e���g�}�b�v�ɂ�闐�������A���S���Y��
�܂����h���A�]�T�̂���Q���҂͈��������e�ȊO�ɂ��l�X�ȃv���O���������R��(�����I��)����Ă��܂����B
- [VB] ���C�t�Q�[��
- [VB] �V���[�e�B���O
- [Ruby] �V���[�e�B���O
- [Ruby] (�����ȒP��)RPG
- [Scheme] sin�̋����W�J�̃O���t�\��
�ɂ��������獡��̍��h�ŎQ�l�ɂ��������A���ꂽ�v���O���������܂Ƃ߂�\��B
- �}2: �g����log���Ƌ����W�J�ŋߎ�����log���̃O���t
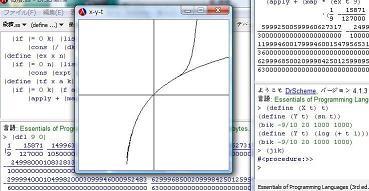
- �}3: �g����sin���Ƌ����W�J�ŋߎ�����sin���̃O���t
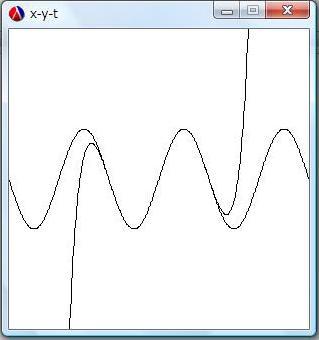
- dsinx.c
- [UDA] sinx��x=�ɂ���������W�������߂�
- sum.c
- [UDA] �Ɏ������閳���a�̌v�Z
- euler.c
- [UDA] �I�C���[�@��x(0)=0,v(t)=cos(t)�̎��Ԕ��W�ׂ�
- kepler.c
- [UDA] RK4�ŃP�v���[���𐔒l�I�ɉ���
- calc_pi.ss
- [UDA] �L�����̎l�����Z�݂̂Ń��v�Z����
- ame.c
- [�����܂�] �����e�J�����@�Ń����߂�
- para.ss
- [@b] Scheme�Ŕ}��ϐ��\���̃O���t��`�悷��
- dif.ss
- [@b] n��������v�Z����
- �}2, �}3�́Adif.ss�ŋ����W�J�̌W�������߁Apara.ss�ŃO���t��`�悵�Ă���l�q
1-3���ڂ̓��e�͎�Ɍ�����w���Ȗځu�����w����_1�v�̓��e���Q�l�ɂ��Ă��܂��BWindows������{�ɂ������h�ƁA�w�Z��Linux������{�ɂ����������ł͓��e�̂��ꂪ���Ƃ���܂����A����̍��h�ŎQ���҂͕������̒P�ʎ擾�ɕK�v�ȍŒ���̃X�L���͐g�ɂ����ƌ�����ł��傤�B�܂�4���ڂ̓��e���A�����Ď��ƂƊ֘A�t����Ȃ�ΑO����ʋ��{�Ȗځu�R���s���[�^�O���t�B�b�N�X���KA�v�œ��l�̓��e�������Ă��܂��B�܂�CG���K��Scheme�łȂ�Ruby���g�p���Ă���̂ŁA���Ȃ菟�肪�قȂ�܂����B
����͊�{���̊�{�𒆐S�Ɉ����܂������A�Q���҂ɂ͂��Ȃ�v���O���~���O�͂����Ă��炦���̂ł͂Ȃ����Ǝv���Ă��܂��B�V�N�x��S2S�̕������ɂ����̂ł܂��m��͂��Ă��܂��A�Ă��܂����h�����Ǝv���܂��i������͖{���ɍ��h�ɂȂ邩���I�H�j�B����Ƃ�S2S����낵�����肢���܂��B
